三角関数の加法定理を、図から導き出してみる。
(α、β、およびα+βが、すべて鋭角の場合)
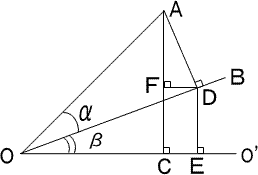
上図で、sin(α+β)は、AC/OAであるので、
OAを基準にして、ACを求めればよいことになる。
A点からOB上に垂線を引く。(D点)
D点からOO'上に垂線を引く。(E点)
D点からAC上に垂線を引く。(F点)
AC=AF+FCであるから、AFとFCを求める。
∠DAFはβであるから、AF=ADcosβ
AD=OAsinαであるから、AF=OAsinαcosβ
FC=DE=ODsinβ
OD=OAcosαであるから、FC=OAcosαsinβ
AC=OA(sinαcosβ+cosαsinβ)
よって、sin(α+β)=sinαcosβ+cosαsinβ
一方、cos(α+β)は、OC/OAであるので、
OAを基準として、OCを求めればよいことになる。
OC=OE-ECであるので、
OE=ODcosβ
OD=OAcosαであるから、OE=OAcosαcosβ
EC=DF=ADsinβ
AD=OAsinαであるから、EC=OAsinαsinβ
OC=OA(cosαcosβ-sinαsinβ)
よって、cos(α+β)=cosαcosβ-sinαsinβ
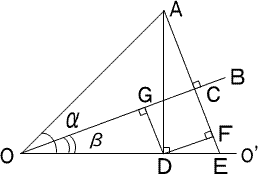
上図で、sin(α-β)はAC/OAであるので、
OAを基準にして、ACを求めればよいことになる。
A点からOB上に垂線を引く。(C点)
A点からOO'上に垂線を引く。(D点)
AC線をOO'に延長する。(E点)
D点からAE上に垂線を引く。(F点)
D点からOB上に垂線を引く。(G点)
AC=AF-FCであるから、AFとFCを求める。
∠DAEはβであるから
AF=ADcosβ
AD=OAsinαであるから、AF=OAsinαcosβ
FC=DG=ODsinβ
OD=OAcosαであるから、FC=OAcosαsinβ
AC=OA(sinαcosβ-cosαsinβ)
よって、sin(α-β)=sinαcosβ-cosαsinβ
一方、cos(α-β)はOC/OAであるので、
OAを基準にして、OCを求めればよいことになる。
OC=OG+GCであるので、
OG=ODcosβ
OD=OAcosαであるから、OG=OAcosαcosβ
GC=DF=ADsinβ
AD=OAsinαであるから、GC=OAsinαsinβ
OC=OA(cosαcosβ+sinαsinβ)
よって、cos(α-β)=cosαcosβ+sinαsinβ