黄金比ともいう。
ある長方形の、短辺と同じ長さの正方形を、
元の長方形から切り取った場合に、
残りの長方形の、長辺と短辺の比率が、
元の長方形の長辺と短辺の比率と同じになる長方形。
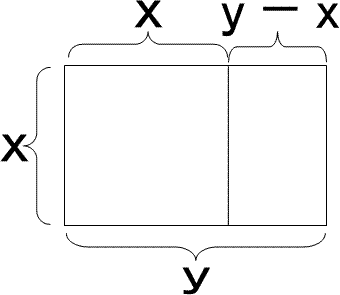
上図から、次の式が書ける。
x:y=(y−x):x
まとめれば、
y(y−x)=x2
比を求めるので、x=1とおく。
y(y−1)=1
あらため、
y2−y−1=0
二次方程式の解と係数の公式をつかい、
y=(−(−1)±√((−1)2−4×1×(−1)))/2×1
計算すると、
y=(1±√5)/2
y≒(1+2.236)/2=1.618
および、
y≒(1−2.236)/2=−0.618
比なので、マイナスの解は無効と考える。
よって、黄金比は、1:1.618 となる。