旝暘偲偼丄傢偐傝傗偡偔偄偊偽丄娭悢偺僌儔僼偺孹偒傪媮傔傞傕偺偱偁傞丅
娭悢偺僌儔僼偺孹偒偼丄倷亖倖乮倶乯偵偍偄偰丄
倶傪旝彫憹壛偝偣偨抣丄倷乫亖倖乮倶亄嚈倶乯偲偺嵎
嚈倷亖倷乫亅倷傪嚈倶偱妱傞偙偲偵傛傝媮傔傜傟傞丅
偮傑傝丄嚈倷乛嚈倶亖乮倖乮倶亄嚈倶乯亅倖乮倶乯乯乛嚈倶偵偍偄偰丄
嚈倶傪嬌尷傑偱彫偝偔偟偨応崌偺抣偱偁傞丅
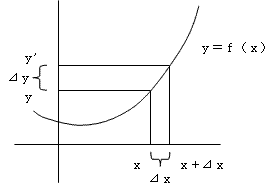
侾丏擇師娭悢丂倷亖倎倶俀亄倐倶亄們丂偵偮偄偰旝暘傪偟偰傒傞丅
丂丂丂丂丂丂丂倷乫亖倎乮倶亄嚈倶乯俀亄倐乮倶亄嚈倶乯亄們丂偲偟丄
嚈倷亖倷乫亅倷亖乮倎乮倶亄嚈倶乯俀亄倐乮倶亄嚈倶乯亄們乯亅乮倎倶俀亄倐倶亄們乯
丂丂丂丂丂丂丂亖倎倶俀亄俀倎倶嚈倶亄倎嚈倶俀亄倐倶亄倐嚈倶亄們亅倎倶俀亅倐倶亅們
丂丂丂丂丂丂丂亖俀倎倶嚈倶亄倎嚈倶俀亄倐嚈倶
忋幃傪嚈倶偱妱傞丅
嚈倷乛嚈倶亖俀倎倶嚈倶乛嚈倶亄倎嚈倶俀乛嚈倶亄倐嚈倶乛嚈倶
丂丂丂丂丂亖俀倎倶亄倎嚈倶亄倐
嚈倶傪嬌尷傑偱僛儘偵嬤晅偗傞偲丄倎嚈倶亖侽偲傒側偣傞偺偱丄
嚈倷亖倓倷丄嚈倶亖倓倶偲昞尰偟偰丄壓婰偺幃偑摼傜傟傞丅
亪倓倷乛倓倶亖俀倎倶亄倐
俀丏嶰妏娭悢丂倷亖倱倝値倶傪旝暘偟偰傒傞丅
嚈倷乛嚈倶亖乮倱倝値乮倶亄嚈倶乯亅倱倝値倶乯乛嚈倶
嶰妏娭悢偺壛朄掕棟倱倝値乮兛亄兝乯亖倱倝値兛們倧倱兝亄們倧倱兛倱倝値兝丂傪棙梡偟丄
嚈倷乛嚈倶亖乮倱倝値倶們倧倱嚈倶亄們倧倱倶倱倝値嚈倶亅倱倝値倶乯乛嚈倶
丂丂丂丂丂亖乮倱倝値倶乮們倧倱嚈倶亅侾乯亄們倧倱倶倱倝値嚈倶乯乛嚈倶
忋幃戞堦崁偺暘曣暘巕偵乮們倧倱嚈倶亄侾乯傪偐偗傞丅
嚈倷乛嚈倶亖乮倱倝値倶乮們倧倱俀嚈倶亅侾乯乛乮們倧倱嚈倶亄侾乯亄們倧倱倶倱倝値嚈倶乯乛嚈倶
倱倝値俀兛亄們倧倱俀兛亖侾傛傝丄們倧倱俀兛亅侾亖亅倱倝値俀兛傪忋幃偵戙擖偟丄
嚈倷乛嚈倶亖乮倱倝値倶乮亅倱倝値俀嚈倶乯乛乮們倧倱嚈倶亄侾乯亄們倧倱倶倱倝値嚈倶乯乛嚈倶
丂丂丂丂丂亖倱倝値嚈倶乛嚈倶乮亅倱倝値倶倱倝値嚈倶乛乮們倧倱嚈倶亄侾乯亄們倧倱倶乯
嚈倶傪嬌尷傑偱僛儘偵嬤晅偗傞偲丄倱倝値嚈倶亖侽丄們倧倱嚈倶亖侾偲傒側偣傞丅
偝傜偵丄嚈倶偑僛儘晅嬤偵偍偄偰偼丄倱倝値嚈倶亖嚈倶偲嬤帡偱偒傞偨傔丄倱倝値嚈倶乛嚈倶亖侾偲側傝丄
嚈倷乛嚈倶亖侾丒乮亅倱倝値倶丒侽乛乮侾亄侾乯亄們倧倱倶乯
丂丂丂丂丂亖們倧倱倶
亪倓倷乛倓倶亖們倧倱倶
俁丏巜悢娭悢丂倷亖倕倶傪旝暘偟偰傒傞丅乮倕偼丄帺慠懳悢偺掙偱倕亖俀丏俈侾俉俀俉丏丏丏偺柍棟悢偱偁傞丅乯
嚈倷乛嚈倶亖乮倕乮倶亄嚈倶乯亅倕倶乯乛嚈倶
丂丂丂丂丂亖倕倶乮倕嚈倶亅侾乯乛嚈倶
偙偙偱丄嚈倶偑僛儘晅嬤偵偍偄偰偼丄倕嚈倶亖侾亄嚈倶偲嬤帡偱偒傞偨傔丄
嚈倷乛嚈倶亖倕倶乮侾亄嚈倶亅侾乯乛嚈倶
丂丂丂丂丂亖倕倶乮嚈倶乛嚈倶乯
丂丂丂丂丂亖倕倶
亪倓倷乛倓倶亖倕倶
係丏懳悢娭悢丂倷亖倢倧倗倕倶傪旝暘偟偰傒傞丅
嚈倷乛嚈倶亖乮倢倧倗倕乮倶亄嚈倶乯亅倢倧倗倕倶乯乛嚈倶
丂丂丂丂丂亖乮倢倧倗倕乮乮倶亄嚈倶乯乛倶乯乛嚈倶
丂丂丂丂丂亖乮侾乛嚈倶乯丒倢倧倗倕乮侾亄嚈倶乛倶乯
嚈倶亖倶倲偲偍偒丄嚈倶仺侽偲偡傞偲偒丄倲仺侽偲偍偗傞偺偱丄
嚈倷乛嚈倶亖倢倝倣倲仺侽乮侾乛倶倲乯丒倢倧倗倕乮侾亄倲乯
丂丂丂丂丂亖倢倝倣倲仺侽乮侾乛倶乯丒倢倧倗倕乮侾亄倲乯乮侾乛倲乯
倲傪尷傝側偔僛儘偵嬤晅偗偨応崌丄乮侾亄倲乯乮侾乛倲乯偼丄抣倕偵廂懇偡傞丅
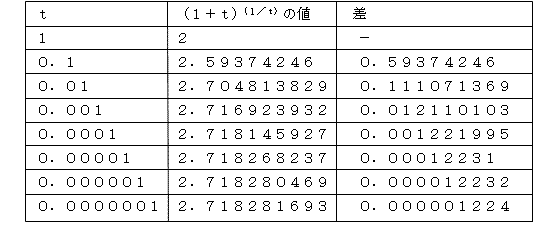
嚈倷乛嚈倶亖乮侾乛倶乯丒倢倧倗倕倕
偙偙偱丄倢倧倗倕倕亖侾偲側傞偺偱丄
亪倓倷乛倓倶亖侾乛倶
俆丏巜悢娭悢丂倷亖倎倶傪旝暘偟偰傒傞丅
倷亖倎倶亖倕倢倧倗倕倎倶亖倕倶倢倧倗倕倎
嚈倷乛嚈倶亖乮倕乮倶亄嚈倶乯倢倧倗倕倎亅倕倶倢倧倗倕倎乯乛嚈倶
丂丂丂丂丂亖倕倶倢倧倗倕倎乮倕嚈倶倢倧倗倕倎亅侾乯乛嚈倶
暘曣暘巕偵丄倢倧倗倕倎傪偐偗傞丅
嚈倷乛嚈倶亖倢倧倗倕倎丒倕倶倢倧倗倕倎丒乮倕嚈倶倢倧倗倕倎亅侾乯乛乮嚈倶倢倧倗倕倎乯
嚈倶倢倧倗倕倎亖倲偲偍偔偲丄嚈倶仺侽偱倲仺侽偲側傞偨傔丄
嚈倷乛嚈倶亖倢倝倣倲仺侽倢倧倗倕倎丒倕倶倢倧倗倕倎丒乮倕倲亅侾乯乛倲
丂丂丂丂丂亖倢倧倗倕倎丒倕倶倢倧倗倕倎丒侾
丂丂丂丂丂亖倢倧倗倕倎丒倎倶
亪倓倷乛倓倶亖倢倧倗倕倎丒倎倶
俇丏懳悢娭悢丂倷亖倢倧倗倎倶傪旝暘偟偰傒傞丅
嚈倷乛嚈倶亖乮倢倧倗倎乮倶亄嚈倶乯亅倢倧倗倎倶乯乛嚈倶
丂丂丂丂丂亖倢倧倗倎乮乮倶亄嚈倶乯乛倶乯乛嚈倶
丂丂丂丂丂亖倢倧倗倎乮侾亄嚈倶乛倶乯乛嚈倶
嚈倶亖x倲偲偍偔偲丄嚈倶仺侽偱丄倲仺侽偲側傞偨傔丄
嚈倷乛嚈倶亖倢倝倣倲仺侽乮倢倧倗倎乮侾亄倲乯乯乛倶倲
丂丂丂丂丂亖倢倝倣倲仺侽侾乛倶丒倢倧倗倎乮侾亄倲乯乮侾乛倲乯
丂丂丂丂丂亖侾乛倶丒倢倧倗倎倕
丂丂丂丂丂亖侾乛倶丒倢倧倗倕倕乛倢倧倗倕倎
丂丂丂丂丂亖侾乛倶丒侾乛倢倧倗倕倎
亪倓倷乛倓倶亖侾乛乮倶倢倧倗倕倎乯
娭悢倷亖倖乮倶乯偵偍偄偰丄倖乮倶乯亖侽偲側傞倶偺抣偼丄僌儔僼偺倶幉偺岎揰偱偁傞丅
偄偭傐偆丄旝暘傪偍偙側偭偨娭悢倓倷乛倓倶亖倖乫乮倶乯偵偍偄偰偼丄
倖乫乮倶乯亖侽偲側傞倶偺抣偼丄倷亖倖乮倶乯偺僌儔僼偺孹偒偑僛儘乮悈暯乯偵側傞揰丄
偡側傢偪丄僌儔僼偺嬌戝丄傑偨偼嬌彫偲側傞揰偑摼傜傟傞丅
偝傜偵旝暘傪偍偙側偆偲乮俀夞旝暘乯丄倓俀倷乛倓倶俀亖倖乫乫乮倶乯偵偍偄偰偼丄
倖乫乫乮倶乯亖侽偲側傞倶偺抣偼丄倷亖倖乮倶乯偺僌儔僼偺孹偒偑丄憹壛偐傜尭彮傑偨偼丄尭彮偐傜憹壛傊偲曄傢傞揰丄
偡側傢偪丄曄嬋揰偑摼傜傟傞丅