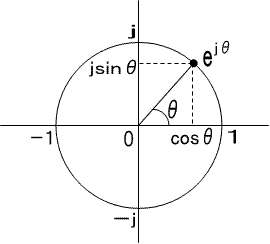
複素平面の単位円を回転するベクトルは、
j2=−1とすると、
(電気の計算では、”i”は、電流を表すため、虚数は、”j”と表記する。)
(”e”は、自然対数の底で、電気の計算では、電圧と区別するため”ε”と表記する場合もある。)
ejθ=cosθ+jsinθ・・・(1)
”θ”を、時間の関数にするため、”ω”を用いる。
(”ω”は角速度。単位=rad/s:ラジアン毎秒)
ω=2πf。ここで、”f”は、周波数(単位=Hz:ヘルツ)とする。
あらためて、θ=ωtとおくと、回転ベクトルは次のように書ける。
ejωt=cosωt+jsinωt・・・(2)
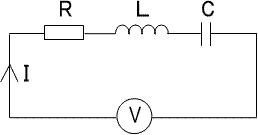
下図の電気回路の、電圧平衡式は、
V=R・I+L・dI/dt+1/C・∫Idt・・・(3)
上記(2)式を用いて交流電流を回転ベクトルで表現し、
”Im”を電流の大きさとすると、I=Im・ejωt
これを、(3)式に代入すると、
V=R・Im・ejωt+L・d/dt・Im・ejωt+1/C・∫Im・ejωtdt・・・(4)
ejωtを”t”で微分すると、jω・ejωt
ejωtを”t”で積分すると、1/jω・ejωt
したがって、(4)式は、次のようになる。
V=R・Im・ejωt+jωL・Im・ejωt+1/jωC・Im・ejωt・・・(5)
(4)式の、微分および積分は、虚数”j”を用いることにより、上記(5)式の通りとなり、
交流電気回路の計算が、代数計算で簡単に行うことができるようになる。
ここで、実数は有効電圧または電流(実際に、回路に流れる電流または電圧)、
虚数は無効電圧または電流(回路に蓄えられるエネルギ)を表すことになる。
また、次のように(5)式を、Im・ejωtでまとめれば、
V=(R+(jωL+1/jωC))Im・ejωt・・・(6)
上記(6)式の係数は、虚数”j”をまとめれば、
Z=R+j(ωL−1/ωC)・・・(7)
電気回路の電圧平衡式(3)は、(6)(7)式により、
V=ZI・・・(8)
となり、交流電気回路でも、オームの法則が成り立っていることがわかる。
(7)式の”Z”は、インピーダンスとよび、交流抵抗を示す。
”Z”は、複素数であるため、その大きさを求める場合、次の通り絶対値をとる。
|Z|=√(R2+(ωL−1/ωC)2)
ωL−1/ωC=0となるように、コイルのインダクタンス”L”(単位=H:ヘンリー)
またはコンデンサのキャパシタンス”C”(単位=F:ファラド)を定めれば、
インピーダンス”Z”は、周波数と無関係になる。
==========
(1)式は、下記のように求める。
f(x)=ax3+bx2+cx+dを微分していく。
f’(x)=3ax2+2bx+c
f’’(x)=3・2ax+2・1b
f’’’(x)=3・2・1a
上式に、x=0を代入すると、各項の係数が求められる。
一般化して、以下の式が書ける。
f(x)=f(0)+f’(0)x+1/(2×1)×f’’(0)x2+1/(3×2×1)×f’’’(0)x3+・・・+1/n!×fn(0)xn
これを、ex、cosx、sinx、にあてはめる。
d/dx・ex=ex
d/dx・cosx=−sinx
d/dx・sinx=cosx
であるから、
ex=1+x+(1/2)x2+(1/6)x3+(1/24)x4+(1/120)x5・・・・
cosx=1−(1/2)x2+(1/24)x4+・・・・
sinx=x−(1/6)x3+(1/120)x5+・・・・
マイナスを合わせるため、”j”を用いる。
jsinx=jx−j(1/6)x3+j(1/120)x5+・・・・
ejx=1+jx−(1/2)x2−j(1/6)x3+(1/24)x4+j(1/120)x5・・・・
したがって、
ejx=cosx+jsinx
が成り立つ。